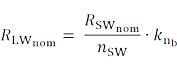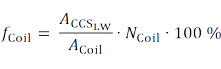В первой половине прошлого века диапазон использования литцендрата соответствовал уровню технологий того времени. Например, в 1923 году первая радиопередача средней частоты стала возможной благодаря использованию литцендрата. В 1940-х годах литцендрат использовался в первых ультразвуковых диагностических системах и базовых системах RFID. В 1950-х годах литцендрат использовался в дросселях USW. Со взрывным ростом новых электронных компонентов во второй половине 20-го века применение литцендрата также быстро расширилось.
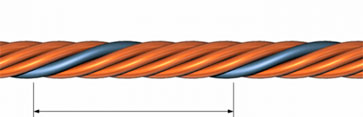
Литцендрат состоит из множества проводов, похожих на канат, разделённых лаковой изоляцией, и используется в широком спектре устройств, требующих хороших характеристик.
Высокочастотные литцендраты изготавливаются с использованием нескольких одиночных проводов, электрически изолированных друг от друга, и обычно используются в устройствах, работающих в диапазоне частот от 10 кГц до 5 МГц.
В катушках, которые являются накопителями магнитной энергии, из-за высоких частот возникают потери на вихревые токи. Потери на вихревые токи увеличиваются с ростом частоты тока. В основе этих потерь лежит скин-эффект и эффект близости, которые можно уменьшить, используя высокочастотный литцендрат. Магнитное поле, вызывающее эти эффекты, компенсируется витой структурой литцендрата.
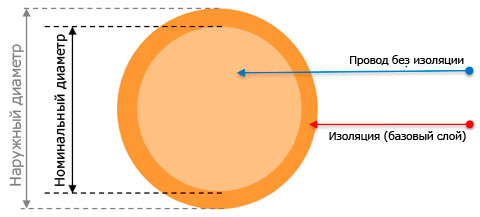
Эмальпровод
Основным компонентом литцендрата является эмальпровод. Для создания литцендрата оптимальной конструкции, возможен выбор эмальпровода с различными свойствами, рассчитанными на разную рабочую температуру. От 130 до 200грд. Также возможно выбрать провод, который легко лудится без зачистки жил от лака.
Схема одинарного провода
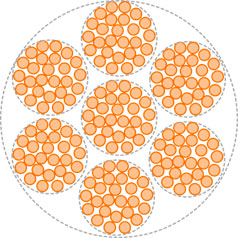
Литцендрат с одноступенчатой скруткой
Необходимое количество одиночных проводов непосредственно скручены в пучок, так что каждый отдельный провод располагается хаотично. Одиночные провода могут занимать любое положение в поперечном сечении литцендрата.
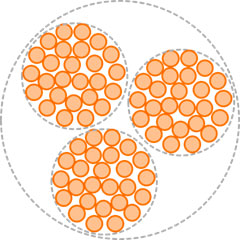
Многоступенчатая скрутка литцендрата
В зависимости от требуемого количества проводников или технических характеристик литцендрат может быть скручен в несколько этапов. Любое количество подготовленных пучков скручивается между собой в несколько этапов скрутки. Электрические и механические свойства конечного продукта зависят от конструкции литцендрата.
Многоступенчатая скрутка в 3 пучка
Многоступенчатая скрутка в 5 пучков
Концентрическая многожильная скрутка с 7 одиночными проводами
Концентрическая многожильная проволока с 7 пучками
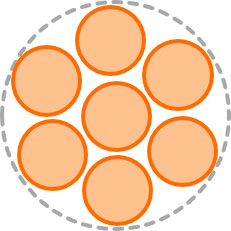
Литцендрат с концентрически расположенными пучками
Отдельные провода располагаются в один или несколько слоев концентрически вокруг центрального проводника литцендрата. При такой конфигурации конструкции каждая отдельная проволока естественным образом перемещается в заданное положение во время скручивания, что приводит к постоянству размеров и рабочих свойств. В качестве центральной жилы может использоваться нить для снятия напряжения.
Шаг скрутки
Шаг скрутки - это расстояние, которое необходимо одному проводу для одного полного оборота по окружности литцендрата (360 градусов).
Шаг скрутки литцендрата
Направление шага
Направление шага указывает на направление скручивания или пучка проволоки в пучковой конструкции. Z-образная скрутка осуществляется по часовой стрелке, а S-образная - в противоположном направлении или против часовой стрелки.
Направление шага скрутки литцендрата
Литцендрат от «Диады»
Компания ДИАДА производит и предлагает широкий ассортимент высокочастотных литцендратов. В связи с различными требованиями, обусловленными широкой областью применения, существует несколько типов литцендрата.
1. Базовый литцендрат
Базовые литцендраты это литцендраты, где провода скручиваются в пучки в один или несколько этапов. Они же служат основой для литцендратов с различными видами покрытий.
2. Изолированный пленкой литцендрат
Дополнительная изоляция может быть добавлена путем обматывания ленты вокруг базового литцендрата. Повышенная диэлектрическая прочность, высокое напряжение пробоя, термическая стойкость, а также гибкость могут быть достигнуты за счет подходящей комбинации материала ленты, количества лент и степени перекрытия лент.
3. Литцендрат с покрытием ферромагнитной пленкой
Этот вид литцендрата используется, в основном, для передачи сигнала, в котором магнитная пленка использована как фильтр от высокочастотных помех, попавших в тракт.
4. Коаксиальный литцендрат
Литцендрат коаксиальной конструкции с внутренней изоляцией из пленки. Наружный слой литцендрата наносится повивом по пленке, изолирующей внутренний литцендрат. Число жил наружного слоя литцендрата совпадает с числом жил внутреннего слоя. Разделитель слоев и наружная оболочка выполняются фторопластовой либо ПЭТ пленкой при необходимости добавляется ферромагнитная пленка
5. Литцендрат повышенной прочности
Очень маленькие литцендраты или литцендраты с высокими требованиями к прочности на разрыв или сроку службы на изгиб могут быть усилены высокопрочной моно- или мультифиламентной нитью. Для достижения наилучших характеристик эти нити размещаются в центре литцендрата. В некоторых случаях достаточно просто встроить нить для снятия напряжения в качестве пучкового непроводящего элемента в литцендрат
Расчет общего сопротивления литцендрата
Общее сопротивление данной конструкции литцендрата определяется удельным сопротивлением материала проводника, номинальным диаметром и количеством отдельных проволок, количеством этапов свивки, выбранной длиной укладки и дополнительными факторами, зависящими от технологического процесса.
Значение сопротивления одиночного провода можно получить из технических данных, предоставленных компанией Диада в таблице ниже.
| Минальный диаметр проволоки, мм | Максимальный диаметр провода, мм | Расчетная масса 1км провода, кг | Минимальное сопротивление 1 м проволоки, Ом | Максимальное сопротивление 1 м проволоки, Ом | ||
|---|---|---|---|---|---|---|
| ПЭТВ-1 | ПЭТВ-2 | ПЭТВ-1 | ПЭТВ-2 | Проволока заданного диаметра | ||
| 0,03 | 0,037 | - | 0,0063 | - | 21,07 | 28 |
| 0,032 | 0,04 | - | 0,0076 | - | 18,66 | 24,39 |
| 0,04 | 0,05 | - | 0,0119 | - | 12,23 | 15,2 |
| 0,05 | 0,062 | - | 0,0182 | - | 7,901 | 9,528 |
| 0,06 | 0,074 | 0,081 | 0,0264 | 0,03 | 6,046 | 6,757 |
| 0,063 | 0,078 | 0,085 | 0,029 | 0,033 | 5,484 | 6,098 |
| 0,071 | 0,088 | 0,095 | 0,0366 | 0,0398 | 4,0375 | 4,8924 |
| 0,08 | 0,098 | 0,105 | 0,0464 | 0,0509 | 3,1232 | 3,7041 |
| 0,09 | 0,11 | 0,117 | 0,0584 | 0,0634 | 2,488 | 2,9015 |
| 0,1 | 0,121 | 0,129 | 0,073 | 0,0774 | 2,0281 | 2,3341 |
| 0,112 | 0,134 | 0,148 | 0,091 | 0,0953 | 1,627 | 1,8485 |
| 0,12 | 0,143 | 0,153 | 0,1037 | 0,1042 | 1,4221 | 1,6042 |
| 0,125 | 0,149 | 0,159 | 0,1129 | 0,1089 | 1,313 | 1,476 |
| 0,13 | 0,155 | 0,165 | 0,122 | 0,1178 | 1,2163 | 1,364 |
| 0,14 | 0,166 | 0,176 | 0,1413 | 0,147 | 1,0552 | 1,1701 |
| 0,15 | 0,176 | 0,19 | 0,1616 | 0,1688 | 0,9191 | 1,0162 |
| 0,16 | 0,187 | 0,199 | 0,1839 | 0,1945 | 0,8098 | 0,891 |
| 0,17 | 0,198 | 0,21 | 0,2072 | 0,2196 | 0,7189 | 0,7875 |
| 0,18 | 0,209 | 0,222 | 0,2315 | 0,2437 | 0,6425 | 0,701 |
| 0,19 | 0,22 | 0,234 | 0,2578 | 0,2713 | 0,6176 | 0,628 |
| 0,2 | 0,23 | 0,245 | 0,2872 | 0,2985 | 0,5221 | 0,5659 |
| 0,21 | 0,243 | 0,258 | 0,3166 | 0,3279 | 0,4742 | 0,5226 |
| 0,224 | 0,256 | 0,272 | 0,3592 | 0,3752 | 0,413 | 0,4579 |
| 0,236 | 0,269 | 0,285 | 0,3986 | 0,4165 | 0,3705 | 0,4116 |
| 0,25 | 0,284 | 0,301 | 0,4462 | 0,4664 | 0,3309 | 0,3659 |
| 0,265 | 0,3 | 0,319 | 0,5008 | 0,524 | 0,2951 | 0,3249 |
| 0,28 | 0,315 | 0,334 | 0,5644 | 0,5807 | 0,2649 | 0,2904 |
| 0,3 | 0,337 | 0,355 | 0,6465 | 0,6666 | 0,2313 | 0,2558 |
| 0,315 | 0,352 | 0,371 | 0,7114 | 0,7075 | 0,2141 | 0,2392 |
| 0,335 | 0,374 | 0,393 | 0,8036 | 0,7999 | 0,184 | 0,2041 |
| 0,355 | 0,395 | 0,414 | 0,9008 | 0,8961 | 0,1688 | 0,1867 |
| 0,38 | 0,421 | 0,441 | 1,0332 | 1,0268 | 0,1437 | 0,1579 |
| 0,4 | 0,442 | 0,462 | 1,1444 | 1,1733 | 0,1299 | 0,1422 |
| 0,425 | 0,469 | 0,489 | 1,2859 | 1,3245 | 0,1153 | 0,1275 |
| 0,45 | 0,495 | 0,516 | 1,4469 | 1,4879 | 0,1017 | 0,1134 |
| 0,475 | 0,521 | 0,543 | 1,6088 | 1,6574 | 0,0926 | 0,1016 |
| 0,5 | 0,548 | 0,569 | 1,7808 | 1,8271 | 0,0827 | 0,0915 |
| 0,53 | 0,579 | 0,601 | 2,0032 | 2,0529 | 0,0738 | 0,0812 |
| 0,56 | 0,611 | 0,632 | 2,2355 | 2,2802 | 0,0662 | 0,0726 |
| 0,6 | 0,653 | 0,676 | 2,5587 | 2,6176 | 0,0584 | 0,063 |
| 0,63 | 0,684 | 0,706 | 2,821 | 2,8723 | 0,0525 | 0,0571 |
| 0,67 | 0,726 | 0,749 | 3,1842 | 3,2486 | 0,0465 | 0,0504 |
| 0,69 | 0,747 | 0,77 | 3,3757 | 3,4454 | 0,044 | 0,0475 |
| 0,71 | 0,767 | 0,79 | 3,5921 | 3,65 | 0,0409 | 0,0455 |
| 0,75 | 0,809 | 0,832 | 3,996 | 4,0646 | 0,0368 | 0,0407 |
| 0,77 | 0,83 | 0,854 | 4,218 | 4,2843 | 0,0349 | 0,0385 |
| 0,8 | 0,861 | 0,885 | 4,2609 | 4,6337 | 0,0324 | 0,0356 |
| 0,83 | 0,892 | 0,916 | 4,8939 | 4,9877 | 0,0301 | 0,0331 |
| 0,85 | 0,913 | 0,937 | 5,1258 | 5,2194 | 0,0288 | 0,0315 |
| 0,9 | 0,965 | 0,99 | 5,6408 | 5,84 | 0,0257 | 0,028 |
| 0,93 | 0,996 | 1,02 | 6,1237 | 6,2358 | 0,0241 | 0,0262 |
| 0,95 | 1,017 | 1,041 | 6,3957 | 6,4954 | 0,0231 | 0,0251 |
| 1 | 1,068 | 1,093 | 7,081 | 7,1857 | 0,0207 | 0,0229 |
| 1,06 | 1,13 | 1,155 | 7,968 | 8,0856 | 0,0189 | 0,0203 |
| 1,08 | 1,151 | 1,176 | 8,271 | 8,3936 | 0,0178 | 0,0196 |
| 1,12 | 1,192 | 1,217 | 8,885 | 9,0116 | 0,0166 | 0,0182 |
| 1,18 | 1,254 | 1,279 | 9,862 | 9,9879 | 0,0149 | 0,0163 |
| 1,25 | 1,325 | 1,351 | 11,051 | 11,1904 | 0,0133 | 0,0145 |
| 1,32 | 1,397 | 1,423 | 12,259 | 12,4613 | 0,012 | 0,013 |
| 1,4 | 1,479 | 1,506 | 13,868 | 14,0306 | 0,0107 | 0,0115 |
| 1,45 | 1,53 | 1,557 | 14,874 | 15,3572 | 0,0099 | 0,0107 |
| 1,5 | 1,581 | 1,608 | 15,88 | 16,0787 | 0,0093 | 0,01 |
| 1,56 | 1,642 | 1,67 | 17,187 | 17,3907 | 0,0086 | 0,0093 |
| 1,6 | 1,683 | 1,711 | 17,992 | 18,2664 | 0,0082 | 0,0088 |
| 1,7 | - | 1,813 | - | 20,5936 | 0,0073 | 0,0078 |
| 1,8 | - | 1,916 | - | 23,1026 | 0,0065 | 0,0069 |
| 1,9 | - | 2,018 | - | 25,7112 | 0,0058 | 0,0062 |
| 2 | - | 2,12 | - | 28,4593 | 0,0053 | 0,0056 |
| 2,12 | - | 2,243 | - | 31,9414 | 0,0047 | 0,0049 |
| 2,24 | - | 2,366 | - | 35,6765 | 0,0042 | 0,0045 |
| 2,36 | - | 2,488 | - | 39,5632 | 0,0038 | 0,004 |
| 2,44 | - | 2,57 | - | 43,1812 | 0,0036 | 0,0038 |
| 2,5 | - | 2,631 | - | 44,3517 | 0,0034 | 0,0036 |
Таблица №1
Общее сопротивление литцендрата можно рассчитать следующим образом:
- номинальное значение сопротивления литцендрата
Где
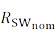– номинальное значение сопротивления одиночного провода
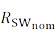– количество одиночных проводов
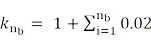– коэффициент укорочения длины в результате процесса скрутки
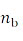– зависящий от количества этапов (шагов) свивки
Максимальное значение сопротивления литцендрата при количестве одиночных проводов более 25:
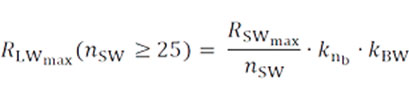
Где
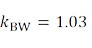– с учетом коэффициента для оборванных проводов
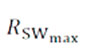– максимальное сопротивление одиночного провода, взятое из справочника
При количестве проводников литцендрата менее 25 коэффициент оборванных проводов kbw не используется.
Расчет наружного диаметра и поперечного сечения Литцендрата
Номинальный наружный диаметр зависит от способа скрутки (прямая, свободная или концентрическая скрутка), количества шагов скрутки, направления шага, длины укладки и выбранного номинального диаметра отдельных проволок. На наружный диаметр также влияют факторы, специфические для данного процесса.
Из-за естественной гибкости литцендрата, радиуса изгиба и стабильности размеров, зависящих от натяжения при скрутке, номинальный внешний диаметр приближенно определяется средним значением в сочетании с определенным методом измерения.
Номинальный наружный диаметр пучковой литцендрата можно рассчитать по следующей формуле:
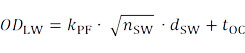
Где kPF – коэффициент заполнения, зависящий от количества проводов, указанный в таблице ниже.
| Коэффициент заполнения KPF | |
|---|---|
| Количество проводов | Коэффициент заполнения |
| От 3 до 12 | 1.25 |
| 16 | 1.26 |
| 20 | 1.27 |
| От 25 до 400 | 1.28 |
Таблица №2
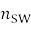– количество одиночных проводов
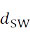– и номинальное значение наружного диаметра одиночного провода
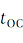– и увеличение диаметра за счет дополнительного внешнего покрытия
Сечение литцендрата, получается из суммы медных сечений отдельных проводов. При этом угол скрутки не учитывается, так как каждый провод изолирован в отдельности
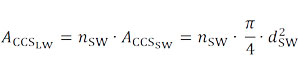
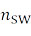– с количеством отдельных проводов
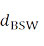– и диаметром одиночного провода без лаковой изоляции (Таблица №1)
Общее сечение литцендрата может быть рассчитано как
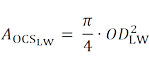с наружным диаметром литцендрата в квадрате
Коэффициенты заполнения
Коэффициент заполнения литцендрата
Коэффициент заполнения литцендрата - это отношение между сечением меди и общим сечением литцендрата.
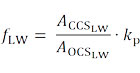
Где
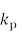– коэффициент специфичный для продукта и процесса его изготовления
Этот коэффициент зависит от выбора номинального диаметра эмальпровода, количества шагов скрутки, шага скрутки, направления шага и толщины изоляционного материала, а также от влияния других параметров процесса.
Коэффициент заполнения литцендрата уменьшается при постоянном общем сечении меди, при уменьшении диаметров отдельных проводов. Так как площадь, связанная с промежуточными воздушными пространствами и эмалью, увеличивается непропорционально, наружный диаметр литцендрата и общее сечение увеличиваются.
То же самое верно для постоянного заданного наружного диаметра, так как здесь, наоборот, поперечное сечение меди должно последовательно уменьшаться.
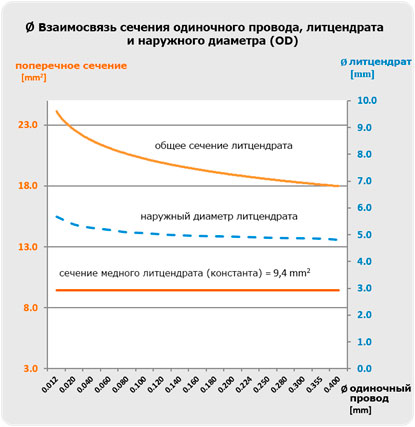
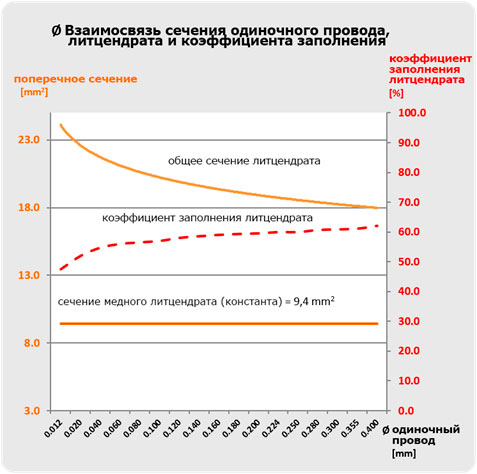
Следующие графики показывают эту зависимость на примере литцендрата с постоянным медным сечением и нескольких одиночных проводов разного диаметра.
График «Взаимосвязь сечения одиночного провода, литцендрата и наружного диаметра (OD)» показывает увеличение OD с ростом номинального диаметра одиночного провода:
График взаимосвязи сечения одиночного провода, литцендрата и наружного диаметра (OD)
График «Взаимосвязь сечения одиночного провода, литцендрата и коэффициента заполнения» иллюстрирует снижение коэффициента заполнения по меди с увеличением номинального диаметра одиночного провода»
График взаимосвязи сечения одиночного провода, литцендрата и коэффициента заполнения
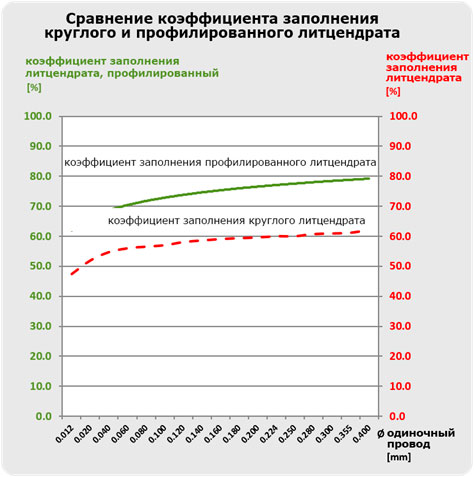
Прокатка круглого литцендрата до квадратного профиля позволяет еще больше увеличить коэффициент заполнения, см. график «Сравнение коэффициента заполнения круглого и профилированного литцендрата», зеленая линия.
График сравнения коэффициента заполнения круглого и профилированного литцендрата
В этом случае более близкое расположение соседних витков позволяет еще раз увеличить коэффициент заполнения катушки. Предпочтительно использовать отдельные провода диаметром толще 0,1 мм, так как литцендрат, изготовленный из более тонких отдельных проволок, более чувствителен к механическим нагрузкам.
Коэффициент заполнения катушки
Этот коэффициент зависит от коэффициента заполнения литцендрата и коэффициента заполнения витков катушки.
Оптимизированный коэффициент заполнения катушки при использовании профилированного литцендрата показан на схеме ниже:
Сравнение коэффициента заполнения катушки с круглым и профилированным литцендратом
Коэффициент заполнения катушки в единицах [%] может быть рассчитан следующим образом
где
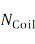– число витков
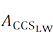– сечение медного литцендрата
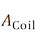– сечение окна обмотки катушки
Основы электромагнетизма
Расчет высокочастотных потерь в Литцендрате
Высокочастотные потери зависят от совокупного влияния различных механизмов потерь, а также от ожидаемых условий работы в конкретном случае. Поэтому простой дифференцированный расчет по формуле невозможен без более глубокого понимания и дополнительных инструментов.
Правило буравчика (правило правой руки)
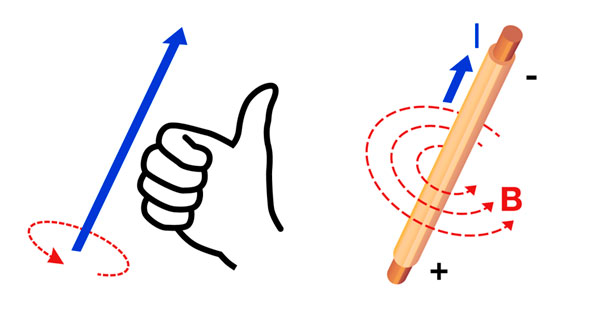
Ток I, текущий по прямому проводнику, создает магнитное поле B, линии поля которого расположены концентрически вокруг проводника. Если прямой проводник взять правой рукой и большой палец направлен в сторону протекающего тока I, то пальцы направлены в сторону кругового магнитного поля В. Величину В называют также плотностью магнитного потока или магнитной индукцией, которая пропорциональна напряженности магнитного поля H и зависящей от материала магнитной проницаемости µ:
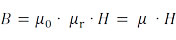
при постоянном магнитном поле, магнитной проницаемости вакуума
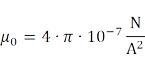
и относительная проницаемость, отношение проницаемости конкретной среды к магнитной проницаемости вакуума.
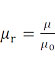
Для иллюстрации смотрите схему «Правило правой руки (правило буравчика)» ниже
Схема правила правой руки (правило буравчика))
Соотношение реактивного сопротивления и сопротивления X/RM
RAC/RDC
Комплексное сопротивление катушки определяется как импеданс Z=R+jX, который является вектором и состоит из сопротивления R, представляющего реальную составляющую, и реактивности X, представляющей мнимую составляющую.
С увеличением частоты, течение тока смещается все больше и больше к внешней поверхности проводника. Измеренное сопротивление переменного тока X, также называемое RAC, возрастает по сравнению с сопротивлением постоянного тока R, иногда называемым RDC.
С увеличением частоты сопротивление переменному току уменьшается, а затем из-за внутренних эффектов, описанных ниже, начинают расти и превышают омические потери при прохождении постоянного тока через литцендрат.
Отношение X⁄R, иногда называемое отношением RAC/RDC, характеризует сопротивление переменного тока, приведенное к сопротивлению постоянного току (X⁄R ≥1), и является показателем высокочастотных характеристик литцендрата. Отношение X⁄R может быть измерено или рассчитано с достаточной точностью в большинстве случаев для данной конструкции литцендрата и желательно, чтобы оно было в пределах 1-1,2 для соответствующего диапазона частот. Наряду с правильным выбором размеров отдельного провода, конструкция литцендрата играет не менее важную роль.
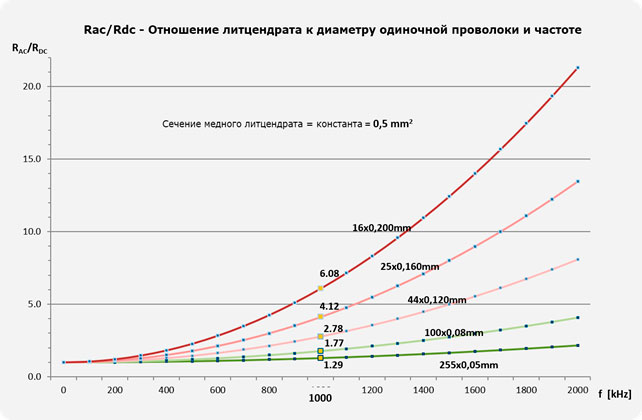
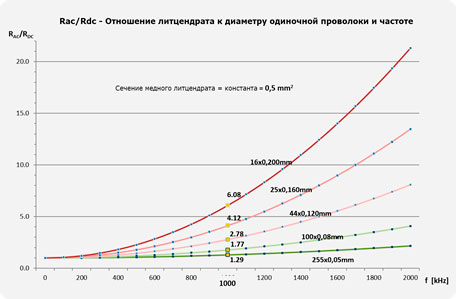
График «RAC/RDC - Соотношение к диаметру одиночной проволоки и частоте» показывает рассчитанную зависимость RAC/RDC от частоты для пяти различных конструкций литцендрата с одинаковой площадью поперечного сечения меди. Он показывает, что сопротивление переменному току и потери переменного тока увеличиваются с ростом частоты и толщины диаметра одиночного провода. На целевой частоте 1 МГц наилучшие результаты показывает конструкция с одножильными проводами толщиной 50 мкм. В этом случае соответствующее отношение RAC/RDC, равное 1,29, все еще значительно выше оптимального значения 1,0. В этом случае, например, первым шагом к улучшению может быть выбор меньшего диаметра одиночного провода и/или оптимизация конструкции пучка.
Отношение литцендрата к диаметру одиночной проволоки и частоте
Коэффициент качества катушки (Добротность катушки)
Коэффициент качества (Добротность катушки) Q измеряет степень свободы от потерь колебательной электрической или механической системы.
Например, более высокий коэффициент Q указывает на меньшую скорость потери энергии относительно запасенной энергии резонатора, колебания затухают медленнее. Маятник, подвешенный на высококачественном подшипнике, колеблющийся в воздухе, имеет высокое значение Q. В то время как маятник, погруженный в масло, имеет низкое значение Q.
В электрическом колебательном контуре, состоящем из воздушной катушки с индуктивностью L, емкостью C и омическим сопротивлением R, коэффициент Q измеряет отношение между полной энергией колебания и потерей энергии на колебание. Важной характеристикой высококачественной системы является использование катушки с высоким Q-фактором.
Основным фактором потерь в катушке является ее сопротивление RL. Сопротивление RL увеличивается с ростом частоты под влиянием зависящего от частоты скин-эффекта и эффекта близости.
Общая взаимосвязь качества может быть описана как
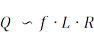
с различными влияющими факторами, которые взаимодействуют друг с другом и приводят к зависимости коэффициента добротности катушки Q от частоты следующим образом
Частота катушки f [Гц]
Коэффициент Q увеличивается с ростом частоты и снова уменьшается в определенный момент из-за непропорционально возрастающих высокочастотных потерь и положительного влияния конструктивных особенностей литцендрата, таких как количество отдельных проводов, номинальный диаметр и шаг скрутки.
Индуктивность катушки L [H]
Коэффициент добротности катушки увеличивается с ростом индуктивности L (т.е. с увеличением числа витков N), отрицательное влияние возрастающих потерь сопротивления катушки R компенсирует этот эффект только на высоких частотах. Собственная емкость катушки увеличивается с ростом числа витков.
Сопротивление катушки R [Ω] зависит от частоты f
На омические потери сопротивления катушки влияет общее сечение проводника ACCS. Уменьшение R первоначально приводит к увеличению коэффициента добротности катушки Q, но на более высоких частотах наступает более сильное снижение коэффициента добротности катушки Q из-за увеличения высокочастотных потерь.
Возможно положительное влияние на коэффициент Q конструкции литцендрата (количество отдельных проволок, номинальный диаметр, длина укладки и т.д.).
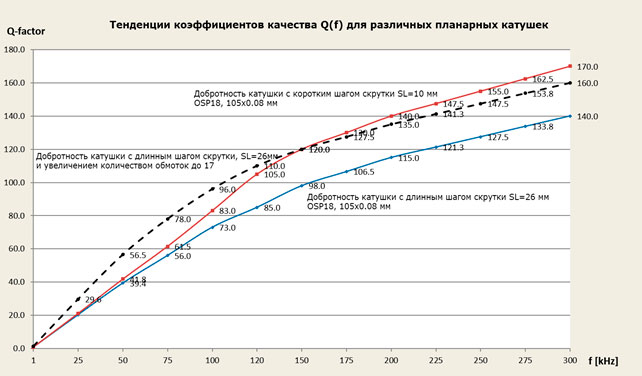
График «Тенденции коэффициентов качества Q(f)» для различных планарных катушек показывает влияние конструкции литцендрата и конструкции катушки на тенденцию коэффициента добротности катушки на примере трех измеренных планарных катушек с 12 витками и различными конструкциями литцендрата.
Тенденции коэффициента качества Q(f)
Уменьшение шага скрутки до (SL) 10 мм, обозначенное на графике красной линией, позволяет увеличить добротность катушки во всем диапазоне частот по сравнению с синей сплошной линией с шагом скрутки (SL) 26 мм. Если увеличение коэффициента добротности катушки необходимо только для выбранного диапазона частот, как в данном примере до 150 кГц, то вместо увеличения шага скрутки может быть достаточно увеличить индуктивность катушки L путем выбора большего числа витков, которые в данном примере находятся в диапазоне от 12 до 17. Здесь коэффициент Q увеличивается для указанного диапазона частот, но падает быстрее для более высоких частот, сравните черную пунктирную линию с красной сплошной линией.
Скин-эффект и глубина скин-эффекта
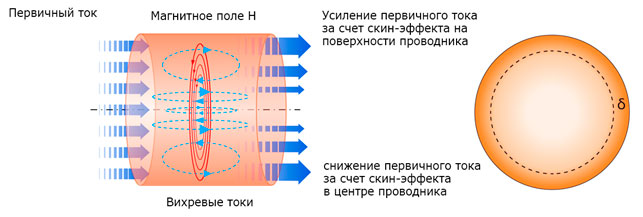
Ток вызывает концентрические магнитные поля, как внутренние, так и внешние по отношению к проводнику. На следующей схеме «Принцип скин-эффекта и глубина скин-эффекта» это представлено напряженностью магнитного поля H.
Часть магнитного поля в самом проводнике создает концентрические и мешающие вихревые токи, которые вызывают смещение течения тока к внешней поверхности поперечного сечения с ростом частоты f. Из-за этого эффекта уменьшается так называемая глубина скин-слоя δ тока, где δ - расстояние от поверхности проводника в центральном направлении, на котором плотность тока уменьшилась до 1⁄e (e= постоянная Эйлера) от амплитудного значения (см. ниже). Таким образом, измеряемое омическое сопротивление становится частотно-зависимым и увеличивается с ростом частоты. Следовательно, тепловые потери увеличиваются пропорционально росту электрического сопротивления.
Принцип скин-эффекта и глубина скин-эффекта
Следующая упрощенная формула описывает скин-эффект только в тех случаях, когда δ меньше или равно трети минимального диаметра проводника и меньше четверти для квадратных конструкций:
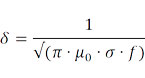
где
μ0 - постоянная, магнитная проницаемость вакуума
σ - проводимость материала проводника
f - частота электрического тока через проводник
В таблице ниже, показана зависимость глубины скин-эффекта от частоты.
| Частота, f | Глубина скин слоя, δ |
|---|---|
| 10 КГц | 0,66 мм |
| 50 КГц | 0,3 мм |
| 100 КГц | 0,21 мм |
| 500 КГц | 0,094 мм |
| 1 МГц | 0,066 мм |
| 10 МГц | 0,021 мм |
| 100 МГц | 0,0066 мм |
Таблица №3
Потери на высоких частотах также вызваны внешним и внутренним эффектом близости.
Эффект близости
Внешний эффект близости
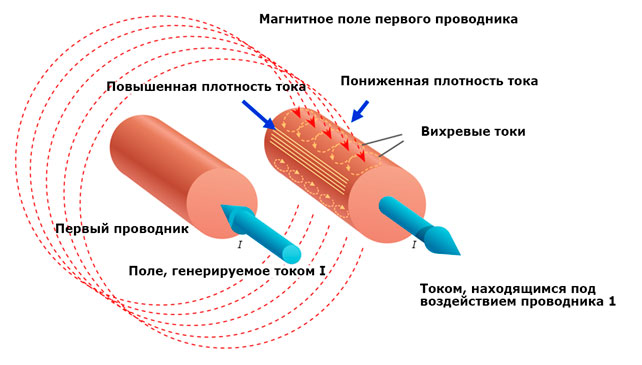
Эффект смещения тока может быть также вызван влиянием внешних переменных магнитных полей соседних проводников или других электрических компонентов, см. иллюстрирующую схему «Внешний эффект близости».
В отличие от вихревых токов, которые индуцируются скин-эффектом, вихревые токи, индуцируемые внешним эффектом близости, не являются вращательно-симметричными относительно центра второго проводника. Причиной этого является переменное магнитное поле первого проводника, которое создается приложенным извне электрическим током через первый проводник.
Внешний эффект близости
Эффект внутренней близости
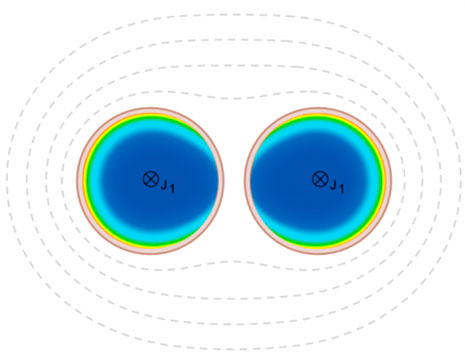
Переменные магнитные поля отдельных проводников литцендрата также создают потери в соседних проводниках за счет вихревых токов. Поскольку эти поля создаются внутри литцендрата самими проводниками, этот эффект называется внутренним эффектом близости, но формально считается относящимся к скин-эффекту, см. схему смещения токов ниже.
Как следствие, электрические потери в литцендрате из-за внутреннего эффекта близости увеличиваются с ростом частоты и в некоторых случаях могут даже превышать потери в одножильном проводнике с таким же сопротивлением постоянному току.
Внутренний эффект близости
На рисунке «Эффект внутренней близости» показано неоднородное распределение тока между соседними одиночными проводами (плотность тока увеличивается от синего к красному цвету).
Этот эффект показывает, что существует оптимальный диапазон частот для литцендрата, в котором потери ниже, чем для одножильного проводника. За пределами этого диапазона использование нескольких одиночных проводов, таких как литцендрат, может иметь негативные последствия.
Скин-эффект и эффект близости являются наиболее важными аспектами при рассмотрении высокочастотных потерь в электрических проводниках, где доминирует совместное влияние внутреннего эффекта близости и внешнего эффекта близости. Для заданной рабочей частоты в большинстве случаев только конструкция из литцендрата может помочь снизить эти потери. В этом случае параметры конструкции, такие как количество одиночных проволок, диаметр одиночной проволоки, количество шагов навивки, шаг скрутки и направление скрутки, должны быть определены для каждого случая применения. В то же время необходимо следить за тем, чтобы каждый отдельный провод занимал каждое место в сечении литцендрата последовательно в пределах определенной длины, чтобы каждый провод сохранял одинаковую длину и сопротивление. В сочетании с эмалированными одиночными проводами литцендрат в данном контексте называется высокочастотным литцендратом (ВЧ).
Диаметр одиночного провода в зависимости от диапазона частот
Дизайн и конструкция высокочастотного литцендрата и его результирующие электрические характеристики зависят от многих факторов. Различные подходы к проектированию могут обеспечить схожие значения характеристик, но для правильного выбора конструкции литцендрата, который может быть изготовлен экономически выгодно и стабильно, требуется опыт. Поэтому правильный выбор диаметра одиночной проволоки и количества пучков и субпучков является важным моментом для каждого конкретного применения.
В таблице «диаметр одиночного провода с оптимальным диапазоном частот», показана зависимость между рекомендуемым диаметром одиночного провода и диапазоном частот.
| Диапазон частот КГц | Диаметр одиночного провода | ||
|---|---|---|---|
| от | до | от | до |
| 0,06 | 1 | 0,4 | 0,254 |
| 1 | 10 | 0,254 | 0,2 |
| 10 | 20 | 0,2 | 0,127 |
| 20 | 50 | 0,127 | 0,102 |
| 50 | 100 | 0,102 | 0,079 |
| 100 | 200 | 0,079 | 0,063 |
| 200 | 350 | 0,063 | 0,05 |
| 350 | 850 | 0,05 | 0,04 |
| 850 | 1400 | 0,04 | 0,03 |
| 1400 | 3000 | 0,03 | 0,02 |
Таблица №4
Расчет потерь в высокочастотных литцендратах
Выбор параметров литцендрата
Конструкция литцендрата - в этом разделе рассматриваются следующие аспекты:
- I Особенности конструкции проводов: Основные влияния конструктивных параметров
- II Выбор диаметра одиночного провода
- III Выбор конструкции пучка
- IV Пример: Литцендрат для намотки ВЧ-слоя
- V Сравнение: Предварительный отбор акк. Чарльз Р. Салливан
Сокращения
AConductor, Litz = общее сечение проводника из литцендрата
Ages,Litz = общее сечение литцендрата
ODLitz = внешний диаметр литцендрата
ODBundle = внешний диаметр пучка
nsw = количество одиночных проводов
ØSW = номинальный диаметр одиночного провода
VF = коэффициент пучка
SL = шаг скрутки
SR = направление шага скрутки пучка
RDC = сопротивление постоянному току
RAC = сопротивление переменного тока
f = частота
ρ = удельное сопротивление проводника
µO = магнитная проницаемость вакуума
δ = глубина скин слоя
J = плотность тока
UBDV = напряжение пробоя
b = ширина окна обмотки
h = высота окна обмотки
NW,tot = общее количество витков
NL = количество слоев обмотки
NW,L = количество витков в каждом слое
FillLitz = коэффициент заполнения медью литцендрата
FillWin = коэффициент заполнения медью окна обмотки
ne = рекомендуемое общее количество одиночных проводов
n1,max = количество одиночных проводов основного пучка на 1-м этапе намотки
k = константа по Ч. Р. Салливану
I Особенности литцендрата: Основное влияние параметров конструкции
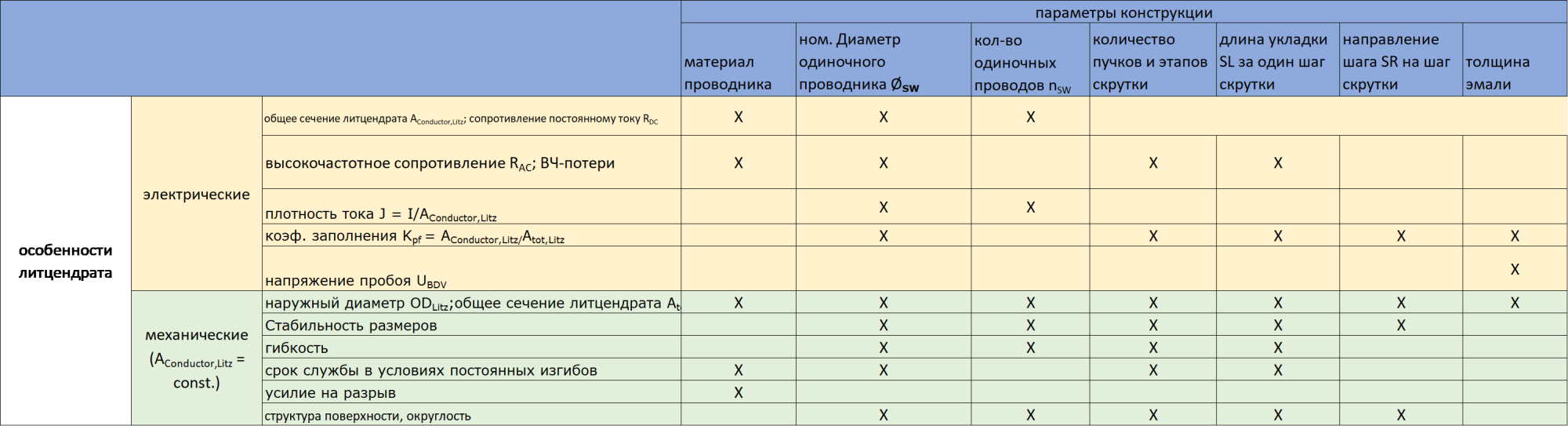
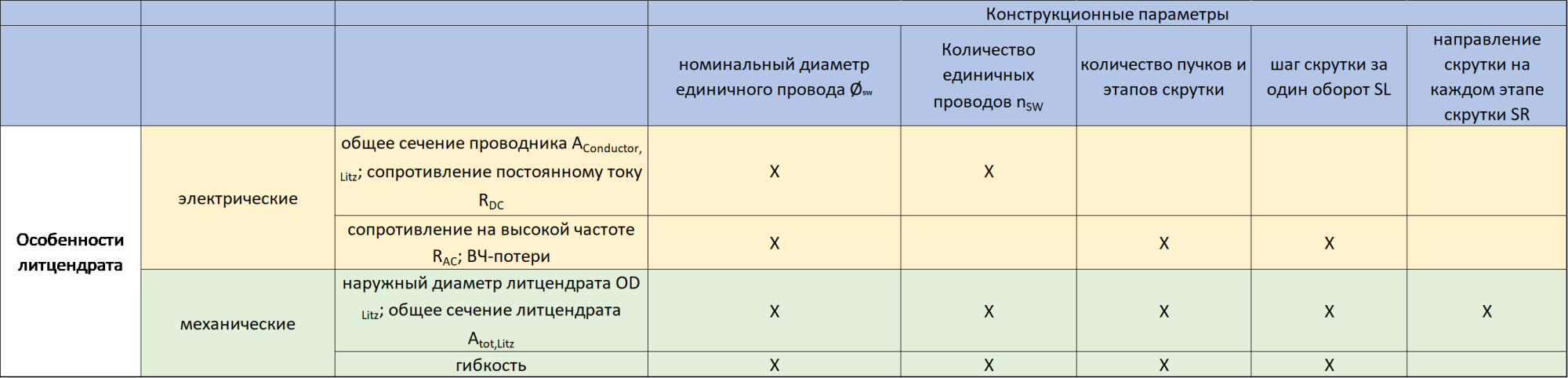
Рабочие характеристики литцендрата определяются его электрическими, механическими, термическими и химическими свойствами. Если термические и химические требования удовлетворяются выбором подходящих изоляционных материалов, например, эмали, то электрические и механические характеристики зависят, прежде всего, от выбранных параметров конструкции пучка.
Таблица №5
Влияние параметров литцендрата на характеристики литцендрата дает представление о взаимном влиянии параметров конструкции на важнейшие электрические и механические характеристики литцендрата.
Таблица №6
Основные влияющие параметры для ВЧ-катушек показывает обзор критериев литцендрата, сведенных к типичным требованиям к высокочастотным катушкам.
Часто в каждой области применения могут быть противоречивые требования, которые должны быть полностью продуманы между компанией ДИАДА и заказчиком. Опыт компании ДИАДА в разработке литцендрата и конструкции литцендрата в сочетании с ожиданиями заказчика по производительности для его применения приводит к получению конечного продукта, демонстрирующего лучшие аспекты производительности, способности к обработке и экономической эффективности.
II Выбор номинального диаметра одиночной жилы
Правильный выбор номинального диаметра одиночной жилы является одним из наиболее важных аспектов при проектировании литцендрата, поскольку он непосредственно влияет на рабочие характеристики литцендрата (см. график соотношения RAC/RDC).
Отношение литцендрата к диаметру одиночной проволоки и частоте
В то же время он влияет на все механические характеристики.
См. таблицу «Влияние параметров литцендрата на характеристики литцендрата».
Таблица №7
Взаимосвязь диаметра одиночной жилы с доминирующей рабочей частотой и ожидаемой глубиной скина устройства показана в таблице.
Смотрите приблизительные значения в таблице:
| Диапазон частот КГц | Диаметр одиночного провода | ||
|---|---|---|---|
| от | до | от | до |
| 0,06 | 1 | 0,4 | 0,254 |
| 1 | 10 | 0,254 | 2 |
| 10 | 20 | 0,2 | 0,127 |
| 20 | 50 | 0,127 | 0,102 |
| 50 | 100 | 0,102 | 0,079 |
| 100 | 200 | 0,079 | 0,063 |
| 200 | 350 | 0,063 | 0,05 |
| 350 | 850 | 0,05 | 0,04 |
| 850 | 1400 | 0,04 | 0,03 |
| 1400 | 3000 | 0,03 | 0,02 |
Таблица №8
В общем, из-за скин-эффекта, чем выше рабочая частота, тем меньше должен быть номинальный диаметр одиночной жилы. Для упрощенного рассмотрения взаимодействия между несколькими диаметрами пучков ODBundle с глубиной скин-слоя δ максимальный диаметр одиночного провода должен быть меньше или равен почти трети δ:
Пример:
f = 200 кГц
δ ≈ 0,172 мм
ØSW ≈ 0,063 мм
Что касается влияния на механические характеристики литцендрата для эквивалентных суммарных сечений меди, то можно предположить следующее:
Чем меньше номинальный диаметр отдельной проволоки, тем
- Литцендрат более мягкий и гибкий
- меньше минимальный радиус изгиба
- лучше характеристики гибкости (выдерживает большее количество перегибов)
- больше общий наружный диаметр литцендрата
- меньше коэффициент заполнения литцендрата
- выше стоимость одной жилы
III Выбор конструкции скрутки литцендрата
Когда количество отдельных проволок определено для конкретного применения, можно выбрать конкретную конструкцию скрутки литцендрата. Более тонкие литцендраты с меньшим числом одиночных проволок свиваются за один шаг, более толстые и сложные литцендраты свиваются за несколько шагов.
Конструкция пучка задается путем определения шага скрутки, направления скрутки пучка (S или Z), а также количеством пучков и шагом скрутки пучков. Правильный выбор параметров пучков необходим для обеспечения оптимальных электрических, механических и технологических характеристик литцендрата (См таблицу ниже)
Таблица №9
Количество пучков и этапов скрутки
Такие параметры, как общее сечение меди, электрическое сопротивление или плотность тока, определяют необходимое количество отдельных проволок, которые могут быть разделены на несколько пучков и этапов скрутки. Поэтому пучки первого шага скрутки могут быть спроектированы для оптимальных высокочастотных характеристик. С учетом этих факторов количество одиночных проводов в одном пучке, обычно, не превышает шестидесяти.
Существует 4 основных конструкции пучков, обычно используемых на последнем этапе формирования пучков: 3, 4, 5 и концентрическая 7-ми пучковая конструкция.
3, 4 и 5 пучковые конструкции
Эти конструкции пучков демонстрируют хорошие характеристики пучков со статистически однородным распределением отдельных проволок по сечению литцендрата. Эти конструкции предпочтительны для оптимальных высокочастотных характеристик. Конструкция с 5 пучками предпочтительна из-за ее круглого профиля, поскольку округлость увеличивается с увеличением числа пучков.
Конструкция литцендрата с 3,4 и 5 пучками
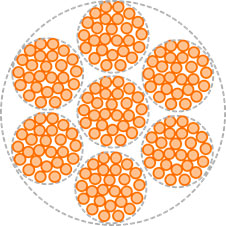
Концентрическая конструкция с 7 пучками
Эти концентрические конструкции, также называемые "1+6 пучков", демонстрируют как высокую гибкость, так и хорошую стабильность размеров и округлость. Один пучок всегда проходит по центру, поэтому такая конструкция менее подходит для применения в условиях, требующих оптимальных высокочастотных характеристик, из-за разницы в полном сопротивлении между пучками. Для того чтобы компенсировать разницу в длине пучков при окончательной скрутке, направление шага центрального пучка противоположно направлению концентрических внешних пучков. Поэтому направление продольного наклона центрального пучка всегда представляет собой направление продольного наклона последнего шага скрутки.
Конструкция литцендрата с 7 пучками (6+1)
Предыдущие базовые конструкции могут комбинироваться друг с другом независимо от количества шагов скрутки и сложности электрических и механических требований. Возможны специальные конструкции.
Выбор шага скрутки и направления шага:
Шаг скрутки определяет механическую компактность и высокочастотные характеристики пучка. Мерой плотности укладки пучка является так называемый коэффициент шага скрутки. Он пропорционален отношению шага скрутки к внешнему диаметру пучка и обычно находится в диапазоне 15-20 мм:
Коэффициент формирования пучков
Коэффициент пучка fB может быть рассчитан как отношение шага скрутки к диаметру пучка следующим образом.
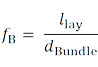
где
llay – шаг скрутки
dBundle – диаметр пучка
В зависимости от направления шага, коэффициент пучка для предварительных шагов пучка часто выбирается выше.
При выборе шага скрутки и направления шага можно исходить из следующих основных положений:
Чем меньше шаг скрутки:
- тем компактнее, жестче и стабильнее по размерам конструкция;
- тем больше внешний диаметр пучка;
- если требуется оптимальная производительность на высоких частотах, необходимо выбрать оптимальную комбинацию согласованных направлений шага скрутки пучков для всех этапов скрутки;
- для сложных конструкций из литцендрата, где требуется высокая механическая гибкость, предпочтительнее использовать встречные направления шагов скруток для нескольких ступеней фомирования литцендрата;
- для намотанных катушек длина укладки должна быть в диапазоне наименьшего диаметра намотки.
| Литцендрат, типономинал | Конструкция | Направление скрутки, SR | Шаг скрутки SL, мм | Коэффициент формирования пучков, fB | Особенности |
|---|---|---|---|---|---|
| 270 × 0.071 мм | (54 × 0.071 mm) × 3 | S,S | 20;26 | ≈ 15 | Хорошие ВЧ-характеристики, грубый текстурированный трехсторонний профиль литцендрата |
| ((30 × 0.071 mm) × 3) × 3 | S,S,S | 20;26;26 | ≈ 20 | Хорошая производительность RF, компактная скрутка | |
| (18 × 0.071 mm) × 3) × 5 | S,S,S | 20;26;26 | ≈ 20 | Хорошие ВЧ-характеристики, компактная скрутка, ровная поверхность и профиль литцендрата | |
| (18 × 0.071 mm) × 3) × 5 | S,S,S | 20;20;26 | ≈ 15 | Прекрасная гладкая поверхность и структура литцендрата | |
| (39 × 0.071 mm) × 7; concen. | S + Z,S | 20 + 20;24 | ≤ 13 | Очень круглый, стабильный по размерам профиль литцендрата, высокая гибкость |
Таблица №10
В таблице представлен обзор различных конструкций литцендрата 270 x 0,071 мм и его особенностей.
IV Пример: Литцендрат для послойной намотки высокочастотных катушек
Во многих случаях высокочастотные катушки наматываются послойно с небольшим количеством витков. Обычно эти литцендраты обматываются шелком или нейлоном, так как точная послойная намотка возможна только с литцендратами, которые сохраняют круглую форму на шпуле катушки и при приложенном натяжении. В некоторых случаях можно использовать и не покрытые литцендраты. Здесь требуется особое внимание к выбору прочных и стабильных по размерам конструкций. Тем не менее, поскольку небольшой эллиптической деформации не избежать, она должна быть компенсирована соответствующим уменьшением общего наружного диаметра. По этой причине при заданном максимальном наружном диаметре в данном случае покрытый литцендрат может показать более высокое сечение меди, чем не покрытая конструкция.
Пример
В примере показан упрощенный предварительный выбор конструкции литцендрата для слоевой обмотки с 30 витками и рабочей частотой 200 кГц. Предполагается, что окно обмотки имеет эффективный полезный размер по ширине и высоте: 25,8 мм x 8,0 мм.
Конструкция слоев
В зависимости от технологии намотки, слоевые обмотки могут быть выполнены в виде слоев с одинаковым или чередующимся количеством витков. Для предварительного выбора возможно грубо рассчитать количество одиночных проводов Литц на слой. В результате для окна обмотки получается 3 слоя по 10 витков в каждом, а расчетный максимальный наружный диаметр закладываемого литцендрата составляет dLW=25,8 мм ⁄ 10 = 2,58 мм.
Диаметр одиночного провода
Чем выше рабочая частота, тем меньше диаметр одиночных проводов. В то же время затраты на эмальпровод будут увеличиваться с уменьшением номинального диаметра dSW, а также на процесс свивки с увеличением сложности конструкции свивки. Что касается взаимодействия между толщиной субпучков и частотно-зависимой глубиной скина δ, отношение dSW ≤ δ/3 может быть принято приблизительно как индикатор для выбора номинального диаметра одиночного провода. На практике он представляет собой рабочий компромисс между частотными характеристиками и стоимостью. В зависимости от условий применения и технических требований допустимы и часто встречаются вариации.
В этом случае номинальный диаметр dSW = 0,063 мм является достаточным для предварительного рассмотрения (см. пример выше, раздел II).
Конструкция пучка
Общий наружный диаметр литцендрата зависит от стабильности размеров отдельных проволок, скрученных в пучки в процессе намотки. Чтобы учесть это как эмпирическое значение, рассчитанный максимальный наружный диаметр изготовленного литцендрата dLW=2,58 мм, см. выше, должен быть уменьшен на 10% до dSW=2,32 мм для покрытого литцендрата и на 15%-20% до dSW=2,19 мм для конструкции литцендрата без покрытия.
Литцендрат без покрытия должен быть скручен компактно, например, это означает небольшую длину укладки и одинаковое направление шага на каждых этапах скрутки. Предпочтительны конструкции с 4 или 5 пучками.
В таблице «Конструкция литцендрата для ВЧ-катушки с определенным окном намотки» показано сравнение подходящих конструкций из покрытого и не покрытого литцендрата для рабочих частот 50 кГц, 125 кГц и 200 кГц и окна намотки шириной x высотой = 25,8 мм x 8,0 мм.
| практический подход | ||||
|---|---|---|---|---|
| Частота | 50 | 125 | 200 | |
| общее количество витков NW,tot | 30 | 30 | 30 | |
| количество слоев NL (слои обмотки) | 3 | 3 | 3 | |
| количество витков на слой NW,L | 10 | 10 | 10 | |
| наружный диаметр литцендрата ODLitz [мм] | с покрытием | 2,19 | 2,19 | 2,19 |
| без покрытия | 2,32 | 2,32 | 2,32 | |
| номинальный диаметр провода в литцендрате ØSW [мм] | 0,100 | 0,080 | 0,063 | |
| Коэффициет заполнения литцендрата FillLitz [%] | с покрытием | 48,20 | 47,70 | 46,10 |
| без покрытия | 47,00 | 46,50 | 44,90 | |
| Коэффициет заполнения окна обмотки FillWind [%] | с покрытием | 25,90 | 26,30 | 24,90 |
| без покрытия | 29,10 | 29,20 | 27,20 | |
| типичная конструкция Литцендрата | с покрытием | 225 x 0.100 mm 5x(45x0.100mm) | 360 x 0.080 mm 5x(4x(18x0.080mm)) | 550 x 0.063 mm 5x(5x(22x0.063mm)) |
| без покрытия | 255 x 0.100 mm 5x(51x0.100mm) | 400 x 0.080 mm 5x(4x(20x0.080mm)) | 600 x 0.063 mm 5x(5x(24x0.063mm)) |
|
Таблица №11
В этом случае для намотки нужного слоя:
- Коэффициент заполнения медью покрытого литцендрата немного меньше по сравнению с литцендратом без покрытия. Количество отдельных проволок и, следовательно, общее медное сечение непокрытого литцендрата все равно увеличивается.
- Коэффициент заполнения медью окна обмотки обычно находится в диапазоне от 25% до 30%. Он выше для покрытого литцендрата по сравнению с непокрытым литцендратом из-за его большего общего сечения меди.
- Конструкция с 5 пучками позволяет получить симметричную структуру литцендрата с пучками значительно меньше, чем 60 одиночных проводов.
Если нет необходимости в послойной намотке и можно использовать произвольно намотанную катушку, то можно получить очень гибкий и мягкий литцендрат. В этом случае витки катушки цепляются друг за друга, промежуточные пространства заполняются оптимально и, таким образом, коэффициент заполнения медью окна обмотки может быть снова увеличен. В качестве альтернативы можно использовать
профилированные литцендраты. Также важно убедиться, что сечение меди в конструкции позволяет достичь требуемой мощности тока для конкретного применения.
V Сравнение: Предварительный отбор по Чарльзу Р. Салливану
Другой метод упрощенного предварительного выбора литцендрата для ВЧ-катушек предложен Чарльзом Р. Салливаном из Школы инженеров Тейера в Дартмуте, США, в его исследовании "Метод упрощенного проектирования литцендрата".
Используемые параметры - это глубина скин-слоя, рабочая частота, число витков окна обмотки, ширина окна обмотки, и из этого рассчитывается постоянная k. Затем этот метод предлагает ряд подходящих конструкций литцендрата, состоящих из номинального диаметра одиночного провода, максимального числа одиночных проводов для первого этапа скрутки и числа пучков для любых дальнейших этапов скрутки.
Этот расчет выполняется на следующими методами:
- Определение глубины скин-слоя δ, рассчитанной на основе удельного сопротивления проводника ρ, рабочей частоты f и проницаемости µ0.
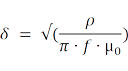
- Определение доступной ширины bW окна обмотки и требуемого количества витков NW для данной конструкции катушки. В качестве опции может быть рассмотрена конструкция с воздушным зазором.
- Расчет приблизительных значений для рекомендуемого общего числа одиночных проводов nSW в зависимости от нескольких номинальных диаметров одиночных проводов dSW. Эффективно применяемое количество одиночных проводов для конкретного номинального диаметра может отклоняться от расчетного значения до ± 25 %.
- Выбор номинального диаметра эмальпровода и количества эмальпроводов. После этого выбора определяется, какой из табличных диаметров одиночных проводов (и комбинаций чисел) в соответствии с заданным числом витков помещается в окно обмотки. Предполагается, что коэффициент заполнения окна обмотки медью составляет от 25% до 30%. Необходимо определить требования к сопротивлению литцендрата и мощности тока. Возможны также альтернативные конструкции с более крупными одиночными проводами.
- Учитывается взаимодействие между глубиной скин-слоя и диаметром пучка: Расчет максимального количества одиночных проводов nSW1max первого шага скрутки зависит от глубины скин слоя δ, зависящей от частоты, и выбранного номинального диаметра одиночного провода dSW.
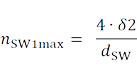
- Часть рассчитанного общего количества одиночных проводов, см. (3), на нескольких комбинациях шага скрутка при 3, 4 и 5 пучковых конструкциях.
В данном контексте не даются рекомендации по длине шага скрутки или направлению пучка в конструкции. Это оставлено на усмотрение производителей литцендрата.
В представленной таблице сравнивается ранее приведенный практический выбор типовых конструкций с выбором конструкций по методу Ч. Р. Салливана. Это относится к катушке с послойной намоткой и окном намотки 25,8 мм х 8 мм и рабочими частотами 50 кГц, 125 кГц и 200 кГц.
| Практический подход | По методу Салливана | |||||
|---|---|---|---|---|---|---|
| Частота f [КГц] | 50 | 125 | 200 | 50 | 125 | 200 |
| Общее количество витков NW,tot | 30 | 30 | 30 | 30 | 30 | 30 |
| Количество слоев (слоев обмотки) NL | 3 | 3 | 3 | 3 | 3 | 3 |
| Количество витков на слой NW,L | 10 | 10 | 10 | 10 | 10 | 10 |
| Наружный диаметр литцендрата ODLitz [мм] | 2,19 | 2,19 | 2,19 | 2,17 | 2,18 | 2,19 |
| Номинальный диаметр | 0,1 | 0,08 | 0,063 | 0,071 | 0,05 | 0,04 |
| Коэффициент заполнения литцендрата FillLitz [%] | 48,2 | 47,7 | 46,1 | 46,9 | 46,1 | 45,2 |
| Коэффициент заполнения окна обмотки FillWind [%] | 25,9 | 26,3 | 24,9 | 25,3 | 25 | 24,6 |
| Типовая конструкция Литцендрата | 225 × 0.100 mm 5×(45×0.100mm) | 360 × 0.080 mm 5×(4×(18×0.080mm)) | 550 × 0.063 mm 5×(5×(22×0.063mm)) | 440 × 0.071 mm 5×(4×(22×0.071mm)) | 875 × 0.050 mm 5×(5×(35×0.050mm)) | 1350 × 0.040 mm 5×(5×(54×0.040mm)) |
Таблица №12
Из таблицы видно, что литцендраты, выбранные с помощью практического подхода, близко соответствуют конструкциям, выбранным с помощью метода Салливана. Они косвенно охватывают рекомендуемые основные характеристики:
- общее количество одиночных проводов в образцах, отобранных практическим путем, находится в диапазоне, предложенном методом Салливана.
- комбинированное применение 3, 4 или 5 пучковых конструкций является составной частью типовых конструкций литцендрата, одиночные провода основных пучков на первом этапе скрутки не зависят от соответствующей конструкции свободно выбираются в пределах 60 одиночных проволок
Снижение затрат возможно при использовании более толстых однопроволочных конструкций (dSW ≤ δ/3), которые демонстрируют, что рекомендуемый Салливаном идеальный базовый пучок ≤ 64 - 36 однопроволочных проводов.
Помимо снижения стоимости эти конструкции могут дополнительно увеличить коэффициент заполнения литцендрата и окна обмотки (см. Таблицу №11).
Благодаря тщательному выбору длины и направления пучков, продукт может быть оптимально подобран для каждого уникального применения.
Поэтому применяемые компанией «Диада» концепции проектирования высокочастотных литцендратов обычно включают как практические, так и теоретические требования.
Тем не менее абсолютно очевидно, что практические условия применения всегда отличаются от идеальных, поэтому мы предлагаем индивидуальный подход к проектированию и изготовлению литцендратов.